 |
 |
 |
| |
| тел:
|
|
 |
| адреc:
|
| 127055
bld.1,
36/1 |
| Novoslobodskaya
str |
| Moskow,
Russia . |
| 127055
Россия, Москва, a/я 35, |
| ул.Новослободская |
| дом
36/1, стр.1 |
 |
| e-mail: |
|
xyz248@xyz248.ru |
|
|
 |
 |
 |
|
 |
|
|
 |
|
 |
 |
 |
 |
Взаимодействие
излучения с веществом:
фундаментальные
проблемы физики и технологии.
Аграфонов
Ю.В., Балахчи А.Г., Бирюлина Т.В., Выговский Ю.Н.1,
Глушков С.М.2,
Исайкин
Ю.Н.
2, Коноп А.Г3,
Коноп С.П. 3,
Кручинин Л.Е.4,
Липов Д.Б.5,
Малов А.Н. .4,
Овчинкин
А.В.
2, Рогаткин Д.А.6,
Тимина О.О. 3,
Ушаков Ф.Е., Фещенко В.С. 3,
Черный В.В.7
Иркутский
государственный университет, г. Иркутск
1-
НТФ “МеДиа”, г. Москва
2-
АОЭиЭ “Иркутскэнерго”, г. Иркутск
3-
Приднестровский государственный университет, г. Тирасполь
4-
Филиал Института Лазерной Физики СО РАН, г. Иркутск
5-
ОАО “Ростелеком”, ТЦМС-12, г. Иркутск
6-
Московский областной научно-исследовательский клинический
институт “МОНИКИ”, г. Москва
7-
Московский институт электроники и математики (МИЭМ), г.
Москва
Введение
Современное развитие исследований в области взаимодействия
излучения с веществом характеризуется широкой многоплановостью
и привлечением практически всех разделов физики для интерпретации
получаемых результатов. Все возрастающая интенсивность деятельности
в этой области фундаментальной физики обуславливается прежде
всего их высокой практической востребованностью для создания
новых информационных, промышленных и медицинских технологий.
Основные
черты современного подхода к проблеме взаимодействия излучения
с веществом связаны с необходимостью учета следующих обстоятельств:
- -
специфических свойств лазерного излучения (когерентность,
монохроматичность, высокая мощность, направленность) и
фотоиндуцированных нелинейных оптических явлений [1, 2].
Можно также отметить, что в целом обработка информации
в любой системе имеет неизбежно пороговый характер (для
минимизации влияния собственных шумов системы) основана
именно на нелинейных явлениях, связанных с малыми неустойчивостями
системы, что, в свою очередь, требует учета даже очень
слабых связей, которые можно назвать информационными [3].
- - сложной
структуры вещества (полимеры, биоподобные вещества и композиции,
синтезированные по методикам молекулярного дизайна) [4,
5]. Структуру сложных веществ и объектов описать исчерпывающим
образом пока невозможно из-за отсутствия ее количественной,
все статистические параметры типа энтропии не позволяют
отслеживать локальную эволюцию вещества под действием
излучения, хотя уже достаточно давно было предложено перенести
формализм теории когерентности и на описание вещества
[1].
- - масштабов
исследуемых явлений, соответствующих области размеров
“пограничных” между классическим и квантово-механическим
описанием системы (биологические системы, волоконно-оптические
системы и оптические информационные устройства, голограммы)
[3, 6].
- - наличие
иерархически связанных фотоиндуцированных структурно-фазовых
переходов и обратных связей, зависящих от действия излучения,
что приводит к возникновению фрактальных и самоорганизующихся
структур в веществе (открытые и неравновесные системы,
коллоидные системы, растворы макромолекулярных веществ,
биологические структуры in vivo ) [2, 7-10].
Основной
проблемой является, конечно, отсутствие единого формализма
для одновременного описания и вещества, и излучения. Особенно
это относится к ситуации, когда явление происходит в области,
являющейся переходной от квантово-механических масштабов к
классическим, что характерно для большинства оптических явлений,
как было недавно показано в современной теории квантовых измерений
[3]. В этом смысле проблема создания теории процесса взаимодействия
излучения с веществом весьма далека от своего решения, если
под таковым понимать тезис Августина Жака Френеля от 1822
г. о том, что “цель всякой хорошей теории должна состоять
в том, чтобы содействовать прогрессу науки открытием связующих
фактов и соотношений между наиболее различными и кажущимися
наиболее независимыми друг от друга категориями явлений” [11].
Одним
из вариантов достижения подобной цели может явиться использование
формализма статистической физики и теории жидкости. Заметим,
кстати, что использование в статистической физике и теории
жидкости теории интегральных, и, в частности, Фурье, преобразований
позволяет говорить об аналогии между явлениями, в них описываемых,
с процессами формирования волновых полей в Фурье-оптике и
применять целый ряд результатов, полученных, например, в компьютерной
оптике [12].
С
квантово-механической точки зрения взаимодействие излучения
с веществом есть резонансное явление, соответствующее равенству
энергии фотона энергии перехода системы. Поэтому всегда необходимо,
при наличии взаимодействия, найти материальную систему с соответствующей
разностью энергий. Это оказывается зачастую нетривиальной
задачей. Так, например, в случае лазерной биостимуляции красным
излучением таких объектов (с химической точки зрения) просто
нет. Скорее всего, это связано с тем, что молекула (в химическом
смысле) не есть минимальная частица живого вещества – она,
конечно, сохраняет химические свойства данного соединения,
но самостоятельно не живет.
Одной
из первых эффективных методик по применению лазеров в медицине
оказалось внутривенное облучение крови (ВЛОК). Форменные элементы
крови обладают высокой конформационной лабильностью и, по-видимому,
способны к кооперативным взаимодействиям, поскольку для продвижения
по микрокапилярным сосудам должны очень сильно деформироваться
[13]. Способность к кооперативным взаимодействиям и объясняет,
по-видимому, возможности крови по “подстройке” к монохроматическому
излучению в широком диапазоне длин волн[8, 13].
От
элементарной (первичной) фотохимической реакции до полного
описания результатов процесса взаимодействия излучения с объектом
лежит достаточно большая дистанция, если иметь в виду реализацию
конкретных информационных или медицинских устройств. Особую
сложность представляет описание поля в рассеивающих, биоподобных
и иных сложно структурированных средах. Если же среда распространения
излучения оказывается “живой” или фоточувствительной (как
в голографии), то ситуация становится почти безнадежной и
может быть разрешена исключительно экспериментально. Также
с большим трудом пока решается проблема описания и исследования
т.н. сингулярных волновых фронтов (спиральных, спекл и дислокационных
пучков излучения); попытки фрактального описания подобных
волновых структур пока не привели к решению задач формирования
полей с заранее заданными параметрами.
Целью
настоящей работы является обзор результатов, полученных коллективом
авторов для различных процессов взаимодействия лазерного излучения
с веществом, и формулировка перспективных направлений исследования
на основе некоторых соображений, приводящихся ниже, применительно
к различным физическим и биологическим системам в порядке
возрастания (по нашему разумению) степени сложности явлений
и процессов.
Исходная
“фотографическая” концепция С точки зрения классической
(и квантовой) электродинамики причины взаимодействия излучения
и вещества связаны с наличием дипольного (или более высокого
порядка) момента у вещества и с достаточной по величине интенсивности
концентрации излучения в этом же месте. Поэтому, с одной стороны,
необходимо знать структуру волнового поля в области взаимодействия,
а, с другой стороны, при наличии факта взаимодействия выяснить
причины образования или наличия дипольного момента. Будем
называть локальные области концентрации поля по интенсивности
сингулярностями излучения, а места локализации дипольного
момента – сингулярностями или центрами светочувствительности
(ЦСЧ) вещества.
В
случае, например, конструирования среды для фотографической
или голографической регистрации информации стремятся достичь
равномерного распределения по всему объему сингулярностей
или ЦСЧ вещества. Это оказывается возможным, если ЦСЧ являются
макромолекулы или их отдельные участки, что характерно для
коллоидных регистрирующих голографических сред и, в некоторой
степени, для биологических объектов, как будет рассмотрено
ниже. Своеобразные ЦСЧ реально могут возникать и естественным
образом, в частности, благодаря граничным слоям жидкости,
как это имеет место вблизи биологических мембран или вблизи
подложки, на которую наносится светочувствительная полимерная
эмульсия. Заметим, что в свое время мембраны предлагалось
рассматривать как основное звено в механизме взаимодействия
КВЧ-излучения с живыми организмами [9], но при этом не в полной
мере учитывалась роль именно граничных структур.
Использование
терминологии и подходов из теории фотографического процесса
[14, 15] нам представляется достаточно удобным и адекватным
для описания процессов взаимодействия излучения со сложными
объектами. За время своего более чем полуторавекового развития
фотографическая наука выработала, хотя и эмпирический, но
практически адекватный формализм типа сенситометрического
описания светочувствительных материалов и процессов, вполне
применимый не только в голографии, но и в биооптике.
Сингулярности
объекта как центры светочувствительности
Граничные
слои и пленочные структуры. Физические
свойства пленок существенно отличаются от свойств объемных
образцов из того же вещества, что связано с влиянием, как
свободной поверхности, так и границы между пленкой и подложкой
на процесс формирования пленки.[16]. Поверхностные и граничные
слои часто характеризуются дальним порядком расположения ориентированных
молекул [17], что ведет к образованию ориентированных квазикристаллических
макроструктур [18]. Экспериментально было установлено еще
в 1930г., что формирование ориентированных граничных слоев
происходит в случае контакта поверхностно-активных веществ
с поверхностью твердого тела. Это обстоятельство широко используется
в способе Ленгмюра-Блоджета для формирования мономолекулярных
слоев полярных молекул на неорганических подложках для сверхразрешающей
нанолитографии [19] и для получения мультимолекулярных слоев
(Y-пленок) [17].
Другим
примером реального использования ориентированных граничных
слоев органических жидкостей являются смазывающие процессы
[17]. Исследования в этой области показали, что силовое поле
твердого тела не экранируется первым слоем молекул жидкости
. Но ориентация молекул полярной жидкости в первом приграничном
к твердой поверхности слое играет роль “затравки”, организующей
ориентацию последующих слоев. Механизмом, реализующим этот
эффект, может являться взаимодействие молекулярных диполей
с образованием нейтральных в целом “цепочек”, перпендикулярных
к поверхности контакта. Подобные соображения стали основой
эмпирической поляризационной теории де Бура и Цвиккера [17],
показавшей как локальное короткодействие, распространяясь
в жидкости путем индуцирования дипольных моментов в соседних
слоях, порождает дальнодействующие силы, упорядочивающие большие
объемы вещества. Поэтому в граничных слоях структура жидкостей
изменяется по сравнению с объемной, и тем сильнее, чем выше
ее полярность и размер молекул растворенного в ней вещества.
В то же время, граничные слои переходят по мере удаления от
твердой подложки в объемную жидкость, что делает актуальной
задачу адекватного описания и этого явления.
Теория
граничных структур. А. Классический подход на основе теории
жидкости. Принципиальная возможность теоретического
исследования структуры неоднородной жидкости вблизи поверхности
определяется нахождением решения совместной системы уравнений
для одночастичной и двухчастичной функций распределения, причем
существуют несколько исходных эквивалентных точных систем
уравнений [20]. Их прямое применение даже для простых систем
сферически - симметричных молекул требует огромных усилий
[21, 22]. Упростить задачу можно, если в уравнении для профиля
плотности вместо анизотропной двухчастичной функции распределения
использовать обычную объемную двухчастичную функцию распределения.
Такая процедура не является однозначной. В зависимости от
того, в какой исходной системе уравнений или каким способом
производится упрощение, можно получить различные синглетные
уравнения для профиля плотности, точность которых можно оценить
лишь по конечным результатам.
Наиболее
распространенным является подход, при котором рассматривается
смесь двух компонент, в которой размеры одной из компонент
становятся как угодно большими. Тогда в пределе нулевой концентрации
этой компоненты функция распределения между двумя компонентами
рассматривается как одночастичная функция распределения ненулевой
компоненты вблизи поверхности. В работе [23] дан анализ существующих
синглетных приближений, из которого видно, что при малых и
средних плотностях все синглетные уравнения являются удовлетворительными.
При больших плотностях, однако, ситуация меняется. Физические
решения имеются лишь для синглетных уравнений, получаемых
из интегральной формы точных уравнений для одночастичной и
двухчастичной функций распределения [24].
Исследование
структуры дипольных систем как в объемном случае, так и тем
более вблизи поверхности усложняется из-за наличия сложной
ориентационной зависимости потенциала взаимодействия между
молекулами. Применение метода интегральных уравнений в среднесферическом
приближении для исследования объемной структуры дипольных
твердых сфер, позволило выразить решение в полуаналитической
форме, в которой угловая зависимость функций распределения
представляется в виде определенных комбинаций тригонометрических
функций. Это решение можно улучшить, используя другие замыкания
уравнения Орнштейна–Цернике. В работе [25] было указано, что
удобной для анализа формой решения является его представление
в виде ряда по степеням параметра диполь - дипольного взаимодействия,
что позволяет, с одной стороны, разделить угловые и радиальные
переменные, с другой — получить зависимость функций распределения
от дипольных моментов в явном виде.
Развиваемый
в [22, 26] подход, в котором также рассматриваются дипольные
твердые сферы у твердой поверхности, отличается в следующих
отношениях: 1. Используется синглетное уравнение, вытекающее
из интегральной формы точного уравнения для одночастичной
функции распределения [24, 25]. Только это уравнение имеет
физическое решение для бездипольных твердых сфер вблизи поверхности
при плотностях выше r=ns3=0.75
. (Здесь n=N/V - численная плотность, s
- диаметр сферы). 2. Решение для одночастичной функции распределения
ищется в виде рядов по параметру диполь- дипольного взаимодействия,
как это было сделано в работе [27] для двухчастичной объемной
функции распределения. 3. Расчеты ограничивались третьим порядком
по параметру диполь- дипольного взаимодействия.
Отметим,
что основной целью теоретического анализа является получение
решений удобных для анализа и описания структурных особенностей,
вызванных действием твердой поверхности на дипольную систему.
Помимо теоретического значения, исследование систем с диполь-
дипольным взаимодействием является важным для анализа структуры
реальных жидкостей. так как наличие ориентационной части потенциала
взаимодействия присуще большинству реальных молекулярных жидкостей.
Точно так же изучение неоднородных систем важно для понимания
свойств жидкости вблизи поверхности твердого тела, взаимодействия
коллоидных частиц, поведения жидкостей в малых объемах.
Развиваемый
подход является по существу одним из вариантов термодинамической
теории возмущений, и ему, конечно, присущи все связанные с
этим ограничения, но он позволяет получить хотя бы качественные
оценки структурных и ориентационных эффектов, а для слабо
дипольных систем предложенный подход является практически
точным. Предложенный подход обладает достаточной общностью,
и применим для описания различных связно-дисперсных систем,
в которых фазы не могут перемещаться свободно, поскольку они
структурно закреплены, например, в гелевой системе. Изложенный
формализм применим для описания широкого класса структурно-граничных
явлений таких, как фазовый переход расплав-кристалл в двухкомпонентной
системе, расчет квантовых поправок к давлению на кривых фазового
равновесия, кристаллизация Леннард-Джонсоновской жидкости
и учет влияния структуры примембранной воды на эффект лазерной
биостимуляции [26].
Б.
Квантово-механический подход
В
физике конденсированного состояния межмолекулярное взаимодействие
входит в гамильтониан в виде амплитуды рассеяния в борновском
приближении. Это приводит к необходимости осуществления перенормировки
взаимодействия. Метод временных функций Грина позволяет вычислять
только спектр элементарных возбуждений, по заданной энергии
основного состояния, определяющему начальные условия для цепочки
функций Грина. Энергия основного состояния определяется диагональными
матричными элементами гамильтониана. Межмолекулярное взаимодействие
входит в гамильтониан в виде амплитуды рассеяния в борновском
приближении.
Для
реальных потенциалов, учитывающих межмолекулярное отталкивание,
борновское приближение непосредственно не применимо. Поэтому
возникает необходимость осуществления перенормировки взаимодействия
с тем, чтобы можно было применить теорию возмущений. Однако
физический смысл констант перенормировки остается неясным.
Целесообразно перейти к такой формулировке теории, в которую
бы исходно входил потенциал межмолекулярного взаимодействия,
а не амплитуда рассеяния. Тем самым термодинамические величины
можно было бы вычислять не прибегая к теории возмущений.
Таким
образом, возникает необходимость рассмотрения жидкостей как
квантовых объектов с учетом сильного межмолекулярного взаимодействия.
Система сильновзаимодействующих фермионов или бозонов может
быть описана с помощью вигнеровских l-частичных
функций. Простейшая из них – двухчастичная функция F12(r1,
p1 ,r2 , p2),
где
ri , pi
- координаты и импульсы частиц. Усредненная по импульсам частиц
функция <F12(r1,
,r2 )>
есть радиальная функция распределения, т.е. плотность вероятности
обнаружения двух частиц в точках с координатами r1,,r2
. Набор l-частичных
вигнеровских функций описывается бесконечной цепочкой зацепляющихся
уравнений Боголюбова. Разработка методов решения таких уравнений
до сих пор остается актуальной задачей. Трудность решения
связана с тем, что необходимо учитывать классические и квантовые
корреляции. Последние спадают с рассеянием гораздо медленнее.
Поэтому обычно ограничиваются либо рассмотрением идеального
квантового газа, либо учет межмолекулярного взаимодействия
осуществляют в методе вторичного квантования в рамках борновского
приближения. Для систем с реальными потенциалами межмолекулярного
взаимодействия борновское приближение неприменимо, поэтому
возникает необходимость перенормировки потенциала.
Вопрос
заключается в том, на каком этапе проводить перенормировку.
Более удобно исходить из вигнеровской формулировки статистической
механики. Уравнения для вигнеровских функций распределения
(частичных матриц плотности) содержат непосредственно потенциал
межмолекулярного взаимодействия. Эволюция функций во времени
описывается бесконечной цепочкой уравнений, аналогичной цепочке
уравнений для функций Грина. Долгое время считалось, что уравнение
для одночастичной функции Вигнера неправильно, так как оно
не описывает квантовый осциллятор. По этой причине вигнеровское
представление не получило широкого применения. Впоследствии
было выявлено, что уравнение для одночастичной функции Вигнера
должно быть дополнено "эволюционным" уравнением, которое должно
правильно учитывать начальные условия. Это обстоятельство
является существенным для вычисления спектра элементарных
возбуждений. Однако для расчета энергии основного состояния
это не имеет значения, так как последняя определяется через
равновесные решения. Поэтому мы предлагаем в основу теории
положить цепочку уравнений для термодинамически равновесных
вигнеровских функций. При этом независимой переменной будет
плотность частиц.
До
сих пор считалось, что решение уравнений для равновесной цепочки
интереса не представляет (и в литературе оно не описано),
так как энергию основного состояния можно найти в рамках теории
нормальной ферми-жидкости Ландау. Однако, реально в таких
вычислениях используется борновское приближение. Таким образом,
предлагаемый подход позволит снять ограничения, связанные
с борновским приближением. А именно, мы предлагаем рассматривать
уравнение для <F12(r1,
,r2 )>
в приближении парных столкновений. В этом случае для <F12(r1,
,r2 )>
получается замкнутое уравнение, которое может быть решено
аналитически. Перенормировка потенциала должна проводиться
именно в этом решении. После такой процедуры возможно получить
обобщение на случай систем с произвольной плотностью по аналогии
с классическим уравнением Орнштейна-Цернике.
В
результате и классические и квантовые системы можно описывать
на основе единого формализма с помощью радиальной функции
распределения, задающей ближний порядок в жидкостях. Такой
подход позволяет описывать термодинамические и структурные
параметры в квантовых газах и жидкостях, в том числе и фазовые
переходы, по заданным плотности, температуре и потенциалу
межмолекулярного взаимодействия.
Взаимодействие
сложных систем с лазерным излучением.
1. Волоконно-оптические линии связи (ВОЛС). Принято считать,
что оптическое волокно (ОВ) является одномерной в геометрическом
смысле системой по отношению к процессам передачи информации.
Но, тем не менее, сама реализация волноводного режима распространения
электромагнитного излучения требует создания соответствующих
трехмерных структур, имеющих, как правило, размеры, сравнимые
с длиной волны излучения [28].
Оптические
волокно и кабель являются достаточно новым промышленным товаром
и их эксплуатационное качество поэтому далеко от параметров
обычных электротехнических изделий. Наряду со стандартными
требованиями к минимизации уровня затухания сигнала в ВОЛС
и в местах состыковки волокон, повышению эффективности ввода-вывода
излучения и др., при эксплуатации системы в условиях, например,
резко континентального климата Восточной Сибири необходимо
учитывать и сложную реакцию всей системы на изменения внешней
среды, и, в особенности, на циклические механо-термические
нагрузки. Характерной особенностью резко континентального
климата является наличие больших температурных суточных колебаний-
до 20 градусов При расположении оптических волокон в грозотросе
ЛЭП размах суточных колебаний может достигать 40 градусов
за счет лучистого солнечного нагрева кабеля и соединительных
муфт. В первые месяцы эксплуатации транссибирской ВОЛС на
работу кабеля стал влиять дефект, проявляющийся как “выдавливание”
стеклянных оптических волокон из пластмассовой защитной оболочки.
Длина освобождающихся при этом участков достигала 100 – 150
мм [29].
Граничные
слои в оптических волокнах. В случае оптических волокон
также могут возникать граничные слои, оказывающие влияние
на процессы распространения когерентного излучения двояким
образом: во-первых, через изменение условий распространения
оболочечных мод, и, во-вторых, через изменение напряженно-деформированного
состояния сердцевины волокна. Поскольку в кабеле грозотроса
ОВ находится для защиты от влияния атмосферной влажности в
гелевом растворе, то всегда вокруг волокна имеются граничные
слои этой гелевой жидкости. Причем их структура существенно
зависит от температуры окружающей среды.
Но
более значительно влияние граничных слоев пластиковой оболочки,
которая наносится на стеклянное или кварцевое волокно при
его изготовлении для защиты от микротрещин. Из самых общих
физических соображений понятно, что вокруг стеклянного ОВ,
обволакиваемого полимерным слоем, формируется коаксиальная
оболочка из упорядоченных макромолекул полимера, которые упорядоченно
укладываются силами адгезии стекло-полимер. При этом структура
такой упорядоченной полимерной оболочки с неизбежностью принимает
спиральную форму. На шаг спирали вдоль волокна, кроме собственных
свойств полимера, влияет и температура всей системы. При циклических
вариациях температуры шаг спирали также циклически меняется,
что приводит к изменению, например, длины и диаметра этой
коаксиальной полимерной оболочке. Очевидно, что коэффициент
термического расширения стекла не обязан совпадать с таковым
для полимера, и рассогласование геометрии сердцевины и оболочки,
даже при очень малой ее величине, может достигать существенных
значений, если учитывать значительную длину “прогонов” в ВОЛС.
Подобный эффект проявляется на концах ОВ, например, в состыковочных
муфтах или в местах сварки волокон и приводит к “выдавливанию”
ОВ из кабеля и возникновению его нежелательных изгибов, которые
повышают затухание сигнала в линии.
Таким
образом, можно констатировать, что основной причиной "выдавливания"
волокон из оболочки является сильное отличие коэффициента
температурного расширения пластиковой оболочки оптического
модуля (ОМ) от параметров оптических волокон (ОВ).С большой
уверенностью можно утверждать, что при изготовлении кабеля
модификация полимера для обеспечения морозоустойчивости была
проведена без дополнительных мер по стабилизации эксплуатационных
свойств полимера. Поэтому при эксплуатации под действием суточных
температурных колебаний через 1-2 месяца происходит значительное
выдвижение волокон из оболочки - до 150 мм. Процесс выдавливания
обусловлен механо-термической деструкцией полимера и имеет
необратимый характер. После окончания основной стадии деструкции
( примерно через 3 месяца ) полимер переходит в стадию физического
и химического старения. При реальной эксплуатации циклическая
термическая деструкция полимера усугубляется и постоянными
микровибрациями ОМ, передающимися от висящего между опорами
грозотроса.
"Выдавливание"
ОВ происходит по механизму "храпового колеса" и инициируется
движением оболочки ОМ, а фиксация выдвинутого волокна относительно
оболочки происходит на витках спирального повива ОВ вокруг
силового элемента ОМ. Поэтому температурные колебания и в
зимний и в летний период будут вызывать дальнейшее развитие
подобного дефекта. Учитывая возможный значительный лучистый
нагрев муфт в летний период можно предположить усиление проявлений
этого дефекта в летнее время. "Выдавливание" волокон из ОМ
имеет статистический характер и поэтому можно утверждать,
что те ОМ и муфты, в которых данный дефект еще отсутствует,
испортятся несколько позже.
Для подавления дефекта в качестве первой меры сейчас предпринимается
перемонтаж соединений в муфтах, а затем будет переработана
конструкция муфт с заменой прямоугольной кассеты на круглую
со спиральной укладкой волокна, обеспечивающей пространственный
запас для размещения выдавленных участков без нежелательных
изгибов. Для полного устранения дефекта необходимо при изготовлении
кабеля использовать полимер, подвергнутый структурной стабилизации
при помощи известных технологических методов (ИК,УФ облучение,
СВЧ-нагрев, введение химических присадок-стабилизаторов и
др.).При этом необходимо, конечно, проведение соответствующих
испытаний в Сибирских условиях. Заметим, что, с другой стороны,
дальнейшее исследование подобных эффектов в волоконных системах
и их анализ может позволить реализовать и сверхчувствительные
датчики физических величин.
Оптика
ОВ с граничными слоями. При распространении излучения
в волокне на его пространственное распределение оказывают
влияние т.н. оболочечные моды ОВ, характеристики которых связаны
с оптическими свойствами среды вне канала передачи излучения.
В рамках физической оптики можно показать, что среди множества
возможных решений волнового уравнения, соответствующих преломленным
и отраженным волнам, есть одна группа, которая соответствует
полному внутреннему отражению для волн приходящих из более
оптически плотной среды. В самой более плотной среде решение
осциллирует и не затухает, а в менее плотной среде амплитуда
волн экспоненциально затухает тем быстрее, чем больше разница
в показателях преломления сред. Таким образом вблизи поверхности
плотной среды существует область, где плотность мощности световой
волны не равна нулю, и, следовательно, световая волна будет
"чувствовать" любые неоднородности материала в этой области,
т.е. свет туннелирует в граничащую среду [28]. Из-за большой
протяженности ОВ искажение вида оболочечных мод может привести
к изменению характеристик линии передачи, а на входных участках
линии, может оказаться существенной и роль нелинейно-оптических
явлений в процессах формирования структуры волноводных мод
ОВ. Поскольку вводимая в ОВ мощность светового сигнала растет
по очевидным соображениям, то и этот вопрос приобретает все
большую и большую актуальность.
Продолжающееся
развитие интегральной оптоэлектроники, волноводной голографии
и интегральной оптики ведет к созданию оптоэлектронных цифровых
микросхем с оптическими входами и выходами и чисто оптических
логических устройств, а, с другой стороны, к развитию технологий
интегрирования пассивных оптических элементов, в том числе
и волоконных, с оптоэлектронными устройствами и созданию полностью
интегральных планарных оптических микросхем [30]. Одним из
первых шагов в этом направлении станут устройства оптических
межсоединений (ОМ), для разработки которых необходимы толстослойные
регистрирующие среды, в которых, в свою очередь, влияние граничных
также окажется значительным. .
И,
наконец, следует отметить еще одно фундаментальное направление
исследований, связанное с влиянием явления формирования граничных
структур на технологию изготовления оптических световодов,
которое пока не получило развития. Хорошо известно, что стекло
является переохлажденной жидкостью [31], поэтому при изготовлении
ОВ из стеклянного расплава неизбежно и формирование концентрических
граничных структур. Можно предположить, что именно с этим
обстоятельством связана и возможность достижения сверхнизкого
уровня затухания светового сигнала в ВОЛС в отличие от массивных
образцов стекла.
2. Коллоидные регистрирующие среды для голографии.
Регистрирующие
среды для голографии обычно представляют собой относительно
тонкие пленки, которые можно описывать как двумерные системы.
Но, аналогично случаю ОВ, для их синтеза и оптических свойств
оказываются существенными все возможные объемные явления и
условия [16, 19, 28].
Формирование
макромолекулярных ЦСЧ в слоях дихромированного желатина. Фотографическая
и голографическая регистрация оптической информации всегда
осуществляется посредством специально организованного фазового
перехода в веществе. Поэтому чем лучше подготовлен фазовый
переход в смысле степени соответствующей инверсии молекул
регистрирующей среды (если ее рассматривать как двухуровневую
квантовую систему), тем выше значение энергетической светочувствительности.
Одновременно должен быть обеспечен и пороговый характер фотохимической
реакции, что необходимо для предэкспозиционного хранения фотоматериала.
Для получения высокой разрешающей способности регистрирующей
среды должно быть выполнено условие пространственной локализации
первичной фотохимической реакции. При выполнении всех этих
требований регистрируемое оптическое излучение играет роль
“курка”, запускающего механизм, желательно самоорганизующийся,
изменения фазового состояния регистрирующей среды на микро
- и макроуровнях.
Механизм
регистрации оптической информации в слоях дихромированного
желатина (ДЖ) может быть представлен как совокупность иерархически
взаимосвязанных фазовых переходов на различных уровнях структурной
организации желатина – внутримолекулярном, молекулярном и
надмолекулярным [32 - 35]. Фотохимические процессы, протекающие
в слое самопроявляющегося (СП) ДЖ, можно рассматривать как
фотостимулированные фазовые конформационные переходы “спираль-клубок”,
приводящие и к изменению макроструктуры слоя, что, в свою
очередь, обеспечивает модуляцию показателя преломления среды
[36]. В качестве светочувствительного агента при этом выступает
ассоциат, который представляет собой тройной комплекс “желатин
- ион Cr(VI) - многоатомный спирт (глицерин)” со своей гидратной
оболочкой. Одной из немаловажных особенностей систем хромированных
коллоидов является локализация как первичных ионов Cr(VI),
так и фотогенерируемых ионов Cr(V) в межпептидном пространстве,
что резко ограничивает диффузию продуктов фотохимической реакции
и, как следствие, обеспечивает высокую разрешающую способность
среды.
Желатин
представляет собой линейный высокоасимметричный полипептидный
полимер белковой природы, ммакромолекулы которого содержат
в среднем 500 - 600 аминокислотных остатков, так что их молекулярная
масса лежит в пределах 40 000 - 100 000. Отличительной чертой
ДЖ, как полимера, является его природное происхождение, а
именно то, что он получается в результате денатурации коллагена,
макромолекулы которого имеют структуру тройной суперспирали.
В силу этого и нативное состояние макромолекулы желатина имеет
биоподобную спирализованную структуру, что позволяет изготавливать
слои ДЖ с исходной упорядоченной – спирализованной – молекулярной
структурой. При синтезе слоя ДЖ (до записи) происходит напряжение
“пружинок” (спирализованных участков макромолекул желатина),
а световое воздействие играет роль “спускового механизма”,
освобождающего эти “пружинки”, которые за счет ранее запасенной
энергии вызывают каскад фазовых изменений состояния желатинового
слоя, обеспечивающих изменение макроскопических характеристик
регистрирующей среды
Желатин
как полимерная система при приготовлении слоя ДЖ проходит
последовательность различных агрегатных состояний. Исходным
состоянием является разбавленный раствор желатина в воде,
в котором макромолекулы находятся в состоянии гауссова клубка
или глобулы [37]. В процессе формования, после полива раствора
на подложку, за счет взаимодействия цепных макромолекул происходит
образование геля, который может иметь свойства жидкого кристалла,
если молекулы являются жесткоцепными, либо свойства концентрированного
раствора. Испарение из политой эмульсии растворителя (воды)
сопровождается процессом возвращения макромолекул в нативное
состояние - типа коллагеноподобной трехтяжной спиральной структуры,
в той или иной степени деформированной условиями пленкообразования-в
первую очередь приграничными к подложке слоями воды. При студенении
под действием подложки и условий сушки происходит развертывание
макромолекул в линейные структуры с одновременным закручиванием
сегментов в спиральные образования. Состояние структурных
элементов в пленке зависит, естественно, от их состояния в
эмульсионном растворе. Так, желатин в пленке, полученной из
раствора при температуре выше 350С,
находится в конформации гауссова клубка без признаков какой-либо
упорядоченности и плоскостной ориентации структурных элементов.
Экспериментально обнаруженная двухканальность первичной фотохимической
реакции, наличие двух типов ионов хрома и двух видов воды
- “свободной” и “связанной” [36] в слоях ДЖ, позволяют предположить,
что фотоструктурные превращения происходят в основном на двух
уровнях: 1) переход “спираль-клубок” в пределах малых участков
полимерной цепи молекулы желатина и 2) изменение структуры
всей полимерной сетки, образующей пленочный квазикристалл
слоя ДЖ.
Ïðè
ýêñïîíèðîâàíèè
ñëîåâ ÑÏÄÆ ïðîèñõîäèò
ðàçâîðà÷èâàíèå
âòîðè÷íîé ñïèðàëè
çà ñ÷åò îñëàáëåíèÿ
ìåæìîëåêóëÿðíûõ
âçàèìîäåéñòâèé
â ñîñòîÿíèå,
áëèçêîå ê êëóáêîâîé
êîíôîðìàöèè,
íî îáëàäàþùåé,
îäíàêî, îïðåäåëåííîé
ñòåïåíüþ óïîðÿäî÷åííîñòè.
 öåëîì, ïðîöåññ
çàïèñè ãîëîãðàìì
â ÑÏ ÄÆ ìîæíî
îõàðàêòåðèçîâàòü
ñëåäóþùèì îáðàçîì:
- Запись оптической
информации происходит путем конформационного изменения вторичной
(переход “спираль-клубок” участка цепи макромолекулы) и
четвертичной (изменение каркаса межмолекулярных связей)
структур желатина, а управление характеристиками этих процессов
эффективно осуществляется на уровнях первичной (химический
состав эмульсии) и третичной (переход “клубок-глобула” для
всей макромолекулы) структур желатиновой системы.
- Центром скрытого
изображения в ДЖ является участок цепи макромолекулы, переходящий
под действием фотовозбужденного иона хрома из спирализованного
в клубковое конформационное состояние. Предельная разрешающая
способность для ДЖ, поэтому определяется величиной куновского
сегмента макромолекулы и составляет 500-2000 ангстрем.
ДЖ
и граничные слои. Однородность оптических свойств
по толщине пленки может играть значительную роль при записи
сверхглубоких голограмм [5], изготовлении волноводных и интегрально-оптических
схем [30] и полутоновых дифракционных оптических элементов
[12]. Неравномерность, например, светочувствительности по
толщине слоя фоторезиста из-за влияния стоячих волн, неизбежно
возникающих при регистрации изображения, может изменять на
50% величину поглощенной фоторезистом энергии, что, в свою
очередь меняет на порядок скорость его проявления , и, как
следствие, ширина линии в проявленном изображении будет варьироваться
с погрешностью ± 0,5 мкм [19]. Это приводит к искажению
записанной структуры, недопустимому с точки зрения практических
применений. С другой стороны, технология синтеза самопроявляющихся
коллоидных систем [32, 34], позволяющая в широких пределах
варьировать как толщину слоев, так и его оптические параметры,
дает новый импульс к исследованию процессов регистрации в
существенно объемных средах и также делает актуальным разработку
новых теоретических подходов и теорий для описания явлений
граничного структурирования в жидкофазных системах.
Адсорбционные
слои жидкости структурируются вследствие ориентации молекул
и притяжения диполей полярных групп соседних макромолекул
[17]. Электростатические силы преобладают при взаимодействии
поверхности с большими частицами, а силы Ван-дер-Ваальса -
с малыми частицами [18]. Структурирование реализуется не только
через электростатическое поле подложки, но и через слоистую
структуру диполей молекул воды или иного растворителя, граничащих
с подложкой. В случае водных растворов белковых макромолекул
типа желатина время формирования граничных слоев водных диполей
лежит в фемтосекундном диапазоне, и поэтому в случае желатиновых
систем эта структурированная вода выступает как специфическое
ориентирующее силовое поле. При этом макромолекулы могут развертываться
в адсорбционном слое таким образом, что гидрофильные части
обращены к водной среде, образуя в ней свободные петли и складки
сегментов цепи. Стабилизация коллоидной системы за счет структурирования
адсорбционных слоев ведет к формированию квазиупорядоченных
гелей, в которых макромолекулы имеют спиральную вторичную
структуру [37], обеспечивающую высокую светочувствительность
самопроявляющегося дихромированного желатина (СПДЖ) [33].
Оптимальную для регистрации оптического излучения структуру
слоя СПДЖ можно, следуя [17], рассматривать как ориентированную
и состоящую из пачек макромолекул ( в отличие от клубков и
глобул [37]). Заметим, что, по-видимому, еще более высокие
голографические характеристики СПДЖ могут быть достигнуты
в мультислойных системах типа Y-пленок [17], обеспечивающих
максимальную планаразацию макромолекул и, следовательно, максимальную
их светочувствительность. Но при этом значительно возрастает
вероятность возникновения проколов пленки и т.н. “фатальных”
дефектов [19].
Важным
фактором, влияющим на свойства СПДЖ как коллоидной системы,
является наличие гидратных оболочек, окружающих полярные группы
макромолекул желатина и создающих упругую водную сетку. Иными
словами, в желатиновом геле имеется “связанная” вода, входящая
в состав сольватных оболочек и обладающая особыми свойствами.
В частности, перестройка квазикристаллической структуры сольватной
оболочки и расслоение фаз [38] играют, несомненно, важную
роль при студенении пленки СПДЖ и при экспонировании.
Поскольку
молекулярный вес макромолекул желатина имеет статистическое
распределение, зависящее от истории приготовления материала,
а сама фотохимическая реакция при экспонировании имеет полихроматический
характер [36], то, очевидно, что адекватная интерпретация
подобных явлений возможна только на основе статистического
подхода.
Сразу
после полива эмульсионного раствора на подложку между макромолекулами
и поверхностью происходят взаимодействия различного типа в
зависимости от энергии химических связей между молекулами
подложки и раствора, от величины поверхностных электрических
полей (возникающих вследствие асимметрии кристаллической решетки
на поверхности), дипольного момента молекул растворителя и
самой регистрирующей среды, температур подложки и раствора
[17, 18]. После приведения в контакт эмульсионного раствора
и подложки молекулы первого будут удерживаться адгезионными
силами, обусловленными поверхностными электростатическими
полями подложки. Дополнительная энергия за счет этих сил делает
возможным движение малых частиц на определенное расстояние
вдоль поверхности или, что характерно для больших органических
макромолекул, их конформационную перестройку до тех пор, пока
избыточная энергия не будет потеряна на атомном остове подложки
и не образуется химическая связь с устойчивым состоянием [18].
В
случае СПДЖ при высоких температурах подложки (более 30о
С) полное время, в течение которого макромолекула движется
вдоль поверхности или перестраивает свое конформационное состояние,
достаточно мало и адсорбированные частицы могут вести себя
как двумерный газ [18]. Но при этом, однако, теряется спиральность
их вторичной структуры, необходимая для записи оптической
информации [33]. Поэтому при поливе слоев СПДЖ целесообразно
обеспечивать низкую температуру подложки, когда макромолекулы
раствора быстро теряют свою избыточную энергию и образуют
устойчивую связь с подложкой (при сохранении спиральности
вторичной структуры), но в этом случае полное время студенения
- формирования гелеобразной структуры слоя - достигает нескольких
суток [34]. Сокращение времени этого процесса возможно при
использовании процедуры лазерного отжига [35].
Первые
макромолекулы желатина обычно захватываются на холодной поверхности
с кинетическими энергиями, зависящими от температуры эмульсионного
раствора, но всегда соответствующими более высоким температурам,
чем у подложки. Перемещаясь по подложке и\или меняя свое конформационное
состояние макромолекула теряет избыточную энергию и конденсируется
в квазитвердое вещество. Конденсация может, в свою очередь,
происходить только, если имеются т.н. зародыши новой фазы,
где частицы могут отдать избыточную энергию. В случае биологических
макромолекул типа желатина ситуация осложняется и наличием
возможности внутримолекулярной конденсации [37]. Высокая концентрация
желатинового раствора может вести к формированию зародышей
в виде “сложенных” цепей (квазикристаллическое состояние)
или “бахромчатой мицеллы” (аналог аморфного состояния) [18].
Когда подложка в достаточной мере заполнена зародышами (зернами),
на них начинают расти т.н. пространственные островки. Если
температура подложки и концентрация раствора малы, то островки
могут формироваться как квазимонокристаллы конденсирующегося
вещества [18,4].При выборе температурного режима приходится
учитывать, что температура перехода “спираль-клубок” для вторичной
структуры макромолекулы в пленке составляет примерно 2/3 от
подобной температуры для объемного материала [14].
Принято
считать [17, 18], что студенение коллоидных макромолекулярных
систем в толстом слое аналогично эпитаксии, — т.е. происходит
ориентированный рост монокристаллических пленок на квазимонокристаллической
подложке, в качестве которой следует рассматривать первый
адсорбированный на твердой поверхности слой макромолекул.
Подобно термически напыленным пленкам, можно предположить,
что при чересчур низкой температуре подложки (менее + 5оС)
практически все макромолекулы желатина случайным образом адсорбируются
на подложку в самых разнообразных конформационных состояниях,
что приводит к образованию аморфной (клубковой) пленки СПДЖ.
Можно предположить также, что, как и при термическом напылении[16],
приложение постоянного электрического поля, параллельного
поверхности, может улучшить однородность формируемой структуры
коллоидных слоев.
3. Взаимодействие низкоинтенсивного лазерного излучения с
биовеществом.
Лазерная
биостимуляция. Феномен лазерной
биостимуляции (ЛБС) широко используется в биологической и
медицинской практике, но его сущность и механизмы еще далеко
не полностью раскрыты и поняты [5, 8]. К основным свойствам
ЛБС обычно относят селективность лазерного воздействия (изменения
индуцируются только в “больных” биосистемах, на “здоровые”
воздействие не оказывается) и то, что эффект наблюдается при
очень малых интенсивностях и поглощаемых энергетических дозах.
Экспериментально было установлено, что лазерное излучение
действует как на биологические клеточные структуры, так и
на отдельную клетку [39]. Попытки установления соответствия
энергетических уровней атомов или молекул с энергией действующего
светового кванта или поиски светочувствительного агента в
биоткани не привели к положительным результатам, что, по-видимому,
связано с недостаточным учетом степени “открытости” биологических
систем. Открытые системы в отличие от идеализированных замкнутых
систем обмениваются со своим окружением веществом, энергией
и, что особенно важно, информацией. Биологические системы
являются не только открытыми, но и состоят из активных малых
объектов, структура которых сложна и недостаточно определена.
По-видимому, конкретизация понятия элемента таких активных
открытых систем существенно зависит от постановки задачи и
требует учета коллективных взаимодействий в процессах самоорганизации,
в отличие от использования понятия “макромолекула”, которое,
по определению, учитывает в первую очередь химические свойства
вещества.
Биологический
объект представляет собой наиболее сложную в оптическом и
структурном отношении систему. В ней, по-видимому, реализуются
все, рассмотренные выше явления, и, кроме того, существенную
роль играют динамические характеристики организма. Двойственность
биосистем, для которых характерны явления, определяемые исключительно
свойствами или отдельных микросистем, их внутренним строением,
или макросистем, но при условии, что они проявляют себя как
целое, и явления, которые не зависят от строения микроскопических
частиц и специфических взаимодействий между ними, а, следовательно,
и от конкретных механизмов протекания процессов. Последние
явления обусловлены интегральными свойствами характеристического
ансамбля с колоссальным числом “безликих” и независимых друг
от друга участников, что описывается в терминах термодинамики
и статистической физики. Несомненную фундаментальную проблему
создает и эволюционно сформировавшееся наличие в нативных
конформациях биологических макромолекул согласованности ближних,
средних и дальних взаимодействий [ 40.]. Ситуацию в биосистемах
усложняют как отсутствие строгой границы между этими явлениями,
так и открытость и неравновесность таких систем.
На
настоящий момент описание явлений, например, в клетке имеет
мозаичный характер: первичный акт взаимодействия фотона с
макромолекулой должен описываться квантомеханически, изменение
конформационного состояния макромолекулы описывается в рамках
квантовой химии и биохимии [ 41], структура макромолекулы
в целом описывается на основе статистической теории П.Флори,
взаимодействие макромолекул описывается в рамках детерминистических
моделей типа “замок-ключ”, “рука-перчатка”, а поведение, например,
клетки в целом описывается на основе теории автоматов и систем
[ 42]. Кроме этого, по мере необходимости, во внимание принимаются
и теории фазовых переходов и самоорганизации [37, 43].
Эффект
ЛБС является нетривиальным примером взаимодействия двух неравновесных
систем: когерентного поля и биологической системы. Несмотря,
казалось бы, на необходимость “резонанса” этих двух систем
по длине волны для возникновения взаимодействия, оно происходит
всегда при монохроматичности излучения, что связано, видимо,
с дискретностью энергетического спектра биосистемы и с изменением
ее параметров во времени - она “дышит” и, тем самым, всегда
обеспечивает резонанс структур. Основными чертами этого взаимодействия
следует считать наличие самоорганизации и эквифинитности -
независимости конечного результата от меняющихся в широких
пределах начальных условий (длина волны, угол освещения, интенсивность
и др.). Предложенный подход показывает, что казалось бы, далекие
друг от друга физические картины типа хаотизации через бифуркации
и теплового нагрева излучением могут быть синтезированы в
едином описании [44].
Механизм
светочувствительности биологических систем. Анализ
явления ЛБС с точки зрения современных физических концепций
приводит к выводам о том, что ,во-первых, процесс содержит
в себе множество различных механизмов воздействия когерентного
излучения на биологические системы, и, во-вторых, к необходимости
рассмотрения процесса ЛБС как самоорганизующегося динамического
взаимодействия открытой, статистически неравновесной, биосистемы
с когерентным излучением, что, в свою очередь, требует учета
взаимодействия динамических и информационных аспектов поведения
сложных систем.
Некоторое
представление о многообразии яалений при взаимодействии сложных
макромолекулярных систем с лазерным излучением может дать
описание эффекта лазерной биостимуляции [39]. Основной чертой
биохимических процессов в клетке является их электронно-конформационный
или матричный характер [41]. Изменения конформационного состояния
макромолекул при, например, их “свертывании” или развертывании,
требуют малых энергий, но приводят к значительным вариациям
в их каталитической активности. Известные модели [42] ферментативного
катализа, такие как “ключ-замок”, “рука-перчатка”, “дыба”
и “белок-машина”, основаны на необходимости обеспечения комплементарности
конформационных состояний субстрата и фермента. Ограниченность
ресурса биомакромолекул в пределах клетки и необходимость
поддержания достаточного для жизнедеятельности количества
макромолекул в заданном конформационном состоянии привели
к возникновению в процессе эволюции специализированного механизма
селекции или перевода молекул в нужное конформационное состояние.
С точки зрения лазерной физики этот механизм можно рассматривать
как систему “накачки”, обуславливающую статистическую неравновесность
всей биосистемы. С квантово-механической точки зрения подобная
неравновесность может рассматриваться как причина когерентного
состояния биовещества и биосистем [1, 7].
Механизм
“накачки” или отбора нужных конформационных состояний макромолекул
может быть описан в рамках теории электромагнитного поля хотя
бы на понятийном уровне, поскольку корректное использование
привычного математического формализма затруднительно. Основной
физической характеристикой биомакромолекулы, связанной с ее
конформационным состоянием, можно считать дипольный и/или
мультипольный момент. Биомакромолекулы взаимодействуют с электрическим
полем световой волны, меняя свое энергетическое состояние
за счет изменения ориентации и величины своего дипольного
момента. Степень эффективности такого взаимодействия можно
оценить параметром a , являющимся мерой потенциальной
энергии диполя 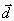 в электрическом поле напряженностью
в электрическом поле напряженностью 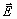 : :
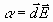 (1) (1)
Следует
отметить, что дипольный (мультипольный) момент биомакромолекул
или ее почти независимых участков - блобов, доменов [37] -
в общем случае отличен от нуля хотя бы из-за наличия температурных
флуктуаций.
Поскольку
любая физическая система стремится к минимизации своей потенциальной
энергии, то можно предположить, что конечный продукт любой
биохимической реакции должен иметь минимальный собственный
дипольный момент хотя бы из-за наличия внутриклеточного поля
ненулевой величины. Поэтому в процессе реакций белкового синтеза
реагенты имеют различные дипольные моменты и поле клетки может
управлять их поведением и, по окончании реакции, они взаимно
компенсируются в максимально возможной степени. Диполь - дипольное
взаимодействие реагентов при синтезе обеспечивает комплементарность
субстрата и фермента, а также обеспечивает более эффективное
по сравнению с конечным продуктом их взаимодействие с электромагнитным
полем лазерного излучения, что ведет к стимуляции различных
реакций синтеза, например, ДНК и РНК [5]. Это можно представить
следующим образом: в результате дипольного взаимодействия
макромолекулы с полем ее энергия повышается, что приводит
к интенсификации процесса “перебора” различных конформационных
состояний и более быстрому “нахождению” комплементарного для
другого реагента конформационного состояния.
Нарушение
функционирования клетки, по-видимому, в первую очередь вызывает
накопление излишних продуктов биологических реакций и для
их выведения за пределы клетки реализуется увеличение поверхностной
площади мембраны, что проявляется как возникновение выпуклостей,
отростков и общей гофризации клеточной мембраны. Попавшая
в такой “карман” объемная клубкообразная биомакромолекула
неизбежно “сплющивается”, становится преимущественно двумерным
образованием, что, в свою очередь, ведет к увеличению ее собственного
дипольного момента А в дипольном приближении эффективность
взаимодействия с электромагнитным полем описывается уравнением
(1). Поэтому рост дипольного момента у молекул приводит к
увеличению ее светочувствительности. Или, иными словами, “болезнь”
сенсибилизирует клетку и обеспечивает селективность ЛБС. Это
простое физическое соображение, хорошо известное, например,
в области синтеза органических фоторегистрирующих сред [19],
объясняет, кроме повышенной эффективности процесса ЛБС для
дефектных клеток, и часть причин, приводящих к различию лазерных
экспериментов в биофизике в условиях in vivo и in vitro. Многочисленные
данные о лазерной стимуляции различных ферментов также, по-видимому,
связаны с подобным уплощением пространственной структуры биомакромолекул,
поскольку каталитический центр многих ферментов также находится
в глубине достаточно узкого “кармана” [42]. Можно заметить,
что клетки, специализирующиеся на фоторецепции, имеют в своем
составе именно плоские структуры типа дисков и ламеллей, что
также подтверждает необходимость “планаризации” структуры
молекулы для повышения ее светочувствительности [41, 42].
Максимальная
амплитуда электрического вектора 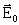 (В/см) световой волны с интенсивностью I (Вт/см2)
определяется выражениям для линейно поляризованного излучения
[2]:
(В/см) световой волны с интенсивностью I (Вт/см2)
определяется выражениям для линейно поляризованного излучения
[2]:
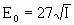 , (2) , (2)
а
для излучения с круговой поляризацией
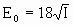 (3) (3)
Из
этих известных соотношений прямым образом следует и наличие
зависимости эффекта ЛБС от характера поляризации лазерного
излучения, даже без учета ориентации клеточной структуры,
что отрицается рядом исследователей [5]. Используя эти соотношения,
можно предположить, что пороговая величина интенсивности лазерного
излучения, еще вызывающая ЛБС, должна быть сравнима с напряженностью
электрического поля, окружающего объект воздействия [39].
Реальные
биосистемы (в т.ч. человек) функционируют в условиях наличия
атмосферного электрического поля, средняя величина которого
составляет около 100 В/м и может значительно меняться в течение
суток - от +600 В/м до -600 В/м, и полей, обусловленных техногенными
факторами. Не конкретизируя механизмов управления биологическими
процессами за счет клеточных электромагнитных полей, можно
предположить, что атмосферное электрическое поле определяет
величину шумов для таких управляющих систем. Поэтому электрическое
поле световой волны, вызывающей ЛБС, должно превышать значение
10-4
мВт/см2
(если считать диэлектрическую проницаемость биоткани равной
50), что соответствует и известным медико-экспериментальным
данным. Корректность введения такого критерия нуждается, конечно,
в сопоставительном анализе данных по ЛБС и данных о напряженности
атмосферного электрического поля во время проведения процедур
лазерной терапии. Также, по-видимому, в качестве критерия
для глубины проникновения лазерного излучения в биоткань следовало
бы использовать величину, соответствующую напряженности атмосферного
электрического поля с учетом диэлектрических свойств биоткани.
Следует
отметить, что дипольное приближение является достаточно грубым
приближением для таких сложных объектов, как биологические
макромолекулы и их объединения, и поле, наводимое ими, будет
иметь в качестве источников так называемые фрактальные токи
конформеров. Характеристики последних определяются конкретными
распределениями процессов пространственно-временной диффузии
продуктов первичной фотохимической реакции и могут быть в
какой то степени описаны в рамках фрактальной теории [39,
45 ]. Дальнейшее описание процесса ЛБС требует учета свойств
биосистемы как своеобразной “машины” и возможно в рамках понятий
нелинейной динамики [39].
Роль
нелинейно-оптических процессов. Лазерное излучение,
попадая на живую ткань, проходит через сложную по структуре
среду, имеющую квазижидкокристаллическое строение. Это обуславливает
сильное изменение пространственного распределения интенсивности
света, что проявляется как в появлении ярких линий-каустик,
так и в возникновении “пятнистой” структуры поля по сечению
пучка - спекл-структуры. Средний размер спекл-пятен и геометрические
характеристики линий-каустик зависят от характеристик среды,
через которую проходит свет и поэтому оказывается, что чем
больший оптический путь пройден светом через биоткань, тем
в большей степени его структурные характеристики - спекл-пятна
и каустики - соответствуют характеристикам биоткани Такой
механизм обратной связи при лазерном облучении обуславливает
неминуемую подстройку фронта световой волны к структуре облучаемой
ткани и объясняет биологическую эффективность ЛБС.
Высокая
когерентность лазерного излучения и фазовый характер взаимодействия
с биотканью приводят к быстрому (на малом отрезке оптического
пути) изменению различных пространственно-временных распределений
интенсивности света. Энергетически значимыми в смысле максимального
воздействия на биоткань при этом оказываются распределения
интенсивности, хорошо согласованные по микроструктуре с участком
облучаемой биоткани Вследствие такой согласованности будет
происходить эффективное возбуждение ансамблей биомакромолекул
либо молекул-рецепторов, передающих свое возбуждение, например,
молекулам нуклеиновых кислот С математической точки зрения
такие процессы можно описывать в рамках фрактальной геометрии
[45], тем более что и биологические ткани допускают также
фрактальное описание. Под фрактальностью биоткани понимают
то, что они имеют при разных масштабах увеличения подобную
геометрическую структуру, которая может иметь дробную (фрактальную)
размерность, а не быть только двух или трехмерной. В терминах
фрактальной геометрии можно сказать, что изменение структуры
светового фронта должно идти до тех пор, пока его фрактальная
размерность не сравняется с фрактальной размерностью облучаемой
биоткани, что обеспечит наилучшие условия возбуждения биологических
структур и макромолекул [46].
Самоподобная
(фрактальная) для разных масштабов рассмотрения пространственно-временная
структура биоткани обуславливает механизм согласования характеристик
электромагнитного поля с оптическими характеристиками среды
при его прохождении через биовещество. “Безучастность” биоорганизма
к облучению естественным светом связана с селективностью реакции
сложной биомолекулы или клетки на воздействие света различных
длин волн. Отсутствие биологического эффекта от естественного
света связано с тем, что в этом излучении энергия, приходящаяся
на частоту, на которую реагирует некоторая выделенная степень
свободы молекулы, слишком мала, чтобы создать существенную
вероятность возбуждения именно такой моды, с которой может
быть связан запуск того или иного биологического механизма,
хотя, в целом, пространственная платность энергии в естественном
свете может быть значительной [9].
Таким
образом, когерентное излучение, попадая в биовещество, изменяет
свое пространственное распределение интенсивности за счет
оптической анизотропии живой ткани. При этом возникают явно
выделенные в пространстве области - каустики, спекл-пятна
- с высокой плотностью мощности лазерного излучения. Можно
показать, что степень фокусировки излучения - величина максимальной
плотности мощности - возрастает с ростом степени когерентности
излучения Высокая плотность мощности излучения в этих областях,
которые к тому же и согласованы по структуре с облучаемой
тканью, обеспечивает возможность возникновения набора компонент
излучения с комбинационными частотами за счет нелинейных эффектов,
присущих живому веществу с квазижидкокристаллической структурой.
Поскольку результирующий биологический эффект в обусловлен
воздействием излучения с комбинационной частотой, которая,
в свои очередь, определяется нелинейными характеристикам биоткани,
то при этом нет критической зависимости от частоты падающего
излучения Важно лишь то, что возникающие комбинационные частоты
имеют дискретный, а не непрерывный спектр. Кратко можно сказать,
что процесс взаимодействия лазерного излучения с живой тканью
является самоорганизующимся: сама ткань меняет пространственные
и частотные характеристики первоначального излучения, которое,
в свою очередь, меняет оптические характеристики ткани за
счет возбуждаемых биологических процессов. Такой подход к
описанию механизма ЛБС примиряет кажущиеся противоречивыми
требования когерентности, независимость терапевтического эффекта
от длины волны когерентного излучения и отсутствие влияния
естественного белого света. В работах сотрудников академика
Н.Д.Девяткова [9] также обсуждались комбинационные частоты
КВЧ-диапазона и отмечалось, что за счет комбинационных явлений
дойти до оптического диапазона частот излучения не удается.
При использовании лазеров ближнего ИК и видимого диапазона
может, по всей вероятности, происходить “спуск” по шкале частот
от оптического диапазона вниз до уровня КВЧ, и при этом нет
запрета на возникновение явлений, хорошо изученных в медицине
при действии КВЧ Такая динамика в качестве одного из своих
аспектов может и должна содержать солитонные механизмы
переноса энергии. зарядов и т.п. Формирование за счет фрактальных
свойств биовещества спектра комбинационных частот когерентного
излучения позволяет по-новому подойти к описанию терапевтического
эффекта при сочетанном ( например, двухволновом) лазерном
облучении биологических объектов и. в частности, попытаться
определить оптимальное соотношение интенсивностей при таком
облучении.. Динамика изменения собственных оптических свойств
живого объекта также, видимо, обеспечивает определенное согласование
излучения со структурой биологической ткани. Пока эта возможность
в более или менее полной мере используется для оценки биологической
активности растительного объекта путем анализа временной декорреляции
спекл-структур, формируемых лазерным излучением при рассеянии
на поверхности объекта [47].
Наличие
иерархичности в многоуровневой структурной организации биологических
систем и результаты последних исследований в области коллоидных
голографических регистрирующих сред указывают на возможность
описания эффекта ЛБС в рамках нелинейно-динамической модели
М.Фейгенбаума. При этом в качестве управляющего параметра
выступает энергия дипольного или мультипольного момента биомакромолекулы
в электромагнитном поле. Большее значение дипольного момента
у “больных” макромолекул приводит к ускорению их движения
к хаотическому состоянию и гибели, а у “здоровых” молекул
ускоряются процессы синтеза, при которых имеются относительно
большие дипольные моменты реагентов. Описание этих явлений
требует также учета свойств масштабного подобия биологических
структур (фрактальности их строения). Использование синергетического
подхода показывает, что процесс взаимодействия лазерного излучения
с биовеществом имеет неадиабатический характер, обусловленный
монохроматическим спектром излучения. Второстепенное значение
при этом имеет абсолютное значение длины волны лазерного излучения.
Существенную
роль при ЛБС играет самоорганизующаяся подстройка пространственно-временного
распределения интенсивности излучения к клеточной структуре
биоткани [39]. Она приводит к тому, что установившееся световое
поле в биоткани практически не зависит от геометрических параметров
падающего волнового фронта. Оказывается, что модовая структура
поля когерентного излучения, распространяющегося в клеточной
структуре, приводит к саморепродукции изображений и “самоисправлению”
элементов структуры поля, что может быть описано в рамках
эффекта Тальбота [48]. На основе модовой теории изображений
и теории информации могут быть определены различия между одномоментным
и сканирующим облучением биоткани в лазерной терапии. Эксперименты
по ЛБС процесса зародышеобразования в растениях подтвердили
значимость периодической структуры поля для повышения степени
стимуляции [49]. Экспериментально обнаружено явление стимуляции
пространственно модулированным лазерным излучением процесса
дифференциации растительных тканей. Пространственная модуляция
лазерного излучения при этом должна соответствовать конкретному
типу растения, а наибольший эффект достигается при освещении
недифференцированных участков ткани излучением, прошедшим
через лист подобного растения. Это позволяет повысить эффективность
и удешевить процесс получения новых гибридов и сортов сельскохозяйственных
культур.
Граничные
слои и структуры при ЛБС. Сэндвичевые структуры дипольных
жидкостей вблизи биомембран [50] также оказываются пространственно
согласованными с самоорганизованным Тальбот-полем лазерного
излучения в биоткани. Из уравнений Боголюбова - Борна - Грина
- Кирквуда - Ивона могут быть получены интегральные уравнения
для профиля плотности воды вблизи поверхности мембраны и описана
структура дипольной системы неоднородной жидкости вблизи поверхности
при наличии сложной ориентационной зависимости потенциала
взаимодействия между молекулами. Чередование водных слоев
с различной преимущественной ориентацией диполей вблизи мембраны
влияет как на процессы свертывания - развертывания белковых
макромолекул, так и на их сенсибилизацию к действию электромагнитного
излучения. Такая структурная организация примембранной жидкости
не позволяет рассматривать процесс ЛБС и как термодинамически
равновесный, а требует привлечения аппарата теории статистической
физики открытых систем. Поэтому, в целом взаимодействие лазерного
излучения с биоструктурами является самоорганизующимся процессом
неадиабатического возмущения системы “мембрана - связанная
вода - биомакромолекулы” и сказывается, в первую очередь,
на эффективности синтеза новых биомолекул [51].
Квантовые
аспекты ЛБС. В работе, на основе современной интерпретации
квантовомеханического подхода показана необходимость учета
информационной открытости биологических систем, участвующих
в процессе ЛБС, которая приводит к нелокальности квантовых
процессов и коллапсам волновых функций в результате “самоизмерений”[3].
Биосистема при этом обладает т.н. запутанной волновой функцией,
описывающей когерентное состояние вещества, что приводит к
нелинейному поведению всей сложной открытой системы, через
которую могут протекать потоки энергии и информации(негэнтропии),
и весь процесс в целом способен поэтому к самоорганизации.
Вследствие этого свойства эффекта ЛБС могут быть объяснены
и смоделированы в рамках обычных физических концепций с привлечением
синергетических представлений.
Как
отмечалось выше, наличие иерархичности в многоуровневой структурной
организации биологических систем указывает на возможность
описания эффекта ЛБС в рамках нелинейно-динамической модели
М.Фейгенбаума. При этом в качестве управляющего параметра
выступает энергия дипольного или мультипольного момента биомакромолекулы
в электромагнитном поле лазерного излучения. Этот механизм
ответственен за ускорение процессов синтеза, например, ДНК
и РНК, в которых участвуют макромолекулы с относительно большими
дипольными моментами. С другой стороны, известна прямая аналогия
между живым организмом и лазером, состоящая в том, что биологический
организм, как и лазер, является нелинейной, упорядоченной
открытой системой, включающей в себя в качестве составных
частей аналоги активной среды, источника накачки и резонатора
[52], и это позволяет надеяться на эффективность использования
формализма квантовой радиофизики для описания эффекта ЛБС.
Заключение.
Резюмируя,
можно сказать, что решение фундаментальной проблемы взаимодействия
лазерного излучения с веществом еще далеко от завершения и
требует дальнейшего развития базисных разделов физики – квантовой
и статистической физики, физической оптики и нелинейной динамики.
Проведенное обсуждение может служить еще одним доказательством
бесспорного тезиса о единстве фундаментальных и прикладных
наук. Разделяя мнение многих уважаемых людей типа М.Планка,
О.Шпенглера и Ф.Энгельса о происхождении современной физики
от паровой машины и промышленной революции, авторы надеются,
что практические потребности, связанные с применением лазеров
хотя бы в ВОЛС и медицине, будут способствовать развитию фундаментальной
физики, по крайней мере, в области взаимодействия излучения
с веществом.
Авторы
выражают благодарность Г.А.Мартынову, Д.С.Сандитову, Г.Н.Саркисову
и А.И.Шварцвальду за многочисленные плодотворные обсуждения
рассмотренных проблем.
Литература
- Делоне Н.Б.
Взаимодействие лазерного излучения с веществом. – М.: Наука,
- 1989. – 280 с.
- Карлов Н.В.,
Кириченко Н.А., Лукьянчук Б.С. Лазерная термохимия. – М.:
ЦентрКом. – 1994. – 368 с.
- Кадомцев Б.Б.
Динамика и информация. 2-е изд. – М.: Редакция журнала “Успехи
физических наук”, 1999. – 400 с.
- Каргин В.А.,
Слонимский Г.Л. Краткие очерки по физико-химии полимеров.
– М.: Химия, 1967. – 232 с.
- Кару Т.И. Фотобиология
низкоинтенсивной лазерной терапии. \ Итоги науки и техники.
Серия физ. Основы лазер. И пучков. Технол. \\ ВИНИТИ. –
1989. – 4.- с. 44 – 84.
- Денисюк Ю.Н.,
Ганжерли Н.М. Псевдоглубокая голограмма, ее свойства и возможные
применения. Л.: ФТИ АН СССР, 1991.- препринт 1519. – 64
с.
- Климонтович
Ю.А. Статистическая теория открытых систем. – М.: ТОО “Янус”,
!((%. – 624 с.
- Илларионов В.Е
Основы лазерной терапии. – М.: РЕСПЕКТ, 1992. – 122с.
- Девятков Н.Д.,
Голант М.Б., Бецкий О.В. Миллиметровые волны и их роль в
процессах жизнедеятельности. – М.: Радио и связь, 1991.
– 168 с.
- Maloletov S.M.,
Kalinkin V.V., Malov A.N., Sherstyuk V.P. On the feasibility
of designing “self-developing” media with high diffraction
efficiency.// Scientific and Applied Photography, (1993),
33, N 3, pp. 448 – 455.
- Планк М.. Принцип
сохранения энергии. М.-Л.:ГОНТИ, 1938. – 236 с.
- Soifer V.A.,
Kotlyar V.V., Doscolovich L.L. Iterative methods for diffractive
optical elements computation/ - London : Taylor&Francis
Ltd., 1997. – 240 p.
- Козлов В.И.,
Мельман Е.П., Нейко Е.М., Шутка Б.В. Гистофизиология капилляров.
– СПб.: Наука, 1994. – 234 с.
- Джеймс Т.Х.
Теория фотографического процесса. – Л.: Химия, 1980. – 672
с.
- Чибисов К.В.
Общая фотография. – М.: Искусство, 1984. – 446 с.
- Броудай М.,
Мерей Дж. Физические основы микроэлектроники.–М: Мир, 1985.–496с.
- Фридрихсберг
Д.С. Курс коллоидной химии –СПб: Химия, 1995.–400с.
- Вундерлих Б.
Физика макромолекул. Т. 1– М: Мир, 1976.–624с., Вундерлих
Б. Физика макромолекул. Т. 2– М: Мир, 1976.–574с.
- Моро У. Микролитография.
В 2-х тт.–М: Мир, 1990.–605+632с.
- Rowlinson J.S.
Widom B. Molecular Theory of Capillarity. - Oxford: Clarendon
Press, 1982.
- Аграфонов Ю.В.,
Тихонов Д.А., Саркисов Г.Н., Мартынов Г.А. Дипольная жидкость
вблизи поверхности. Метод теории возмущений. Синглетное
приближение. // Коллоидный журнал, 1992, т. 54, № 1, стр.
3-13.
- Аграфонов Ю.В.
Структура жидкости вблизи твердой цилиндрической поверхности.
// Коллоидный журнал, 1994, т. 56, № 4, стр. 473-476
- Тихонов Д.А.,
Аграфонов Ю.В. Мартынов Г.А. и др. //Коллоид. Журн. 1991.
Т.53.№5.с.911
- Мартынов
Г.А. Проблема фазовых переходов в статистической механике.
УФН, 169,
№ 6, с. 595 – 624.
- Саркисов
Г.Н. Приближенные уравнения теории жидкостей в статистической
термодинамике классических жидких систем. УФН, 169,
№ 6, с. 625 – 642.
- Аграфонов
Ю.В., Балахчи А.Г., Бирюлина Т.В., Выговский Ю.Н., Дорогобид
Я.С., Кручинин Л.Е., Малов А.Н., Ушаков Ф.Е., Черный В.В.
Граничные структуры жидкости и голографические регистрирующие
среды.. \\ Компьютерная оптика, (1999), вып. 19, с. 118
– 124.
- Agrafonov Yu.V.,
Martynov G.A., Sarkisov G.N. //Molecular Physics. 1980.
V. 39. N 4. P. 963.
- Солимено С.,
Крозиньяни Б., Ди Порто П. Дифракция и волноводное распространение
оптического излучения. М., Мир, 1989, 664 стр
- Аграфонов Ю.В.,
Липов Д.Б., Малов А.Н., Овчинкин А.В.. Проблемы эксплуатации
волоконно-оптических систем связи. \\ Компьютерная оптика,
(1999), вып. 19, с. 159 – 164.
- Баблумян А.С.,Морозов
В.Н.,Путилин А.Н.,Шермергор Т.Д. Волноводные голограммы
в системах передачи, хранения и обработки информации //
Труды ФИАН,1987,т.185,с.164-190./перевод Proceedings of
Lebedev Physics Institute, Ac.Sc.USSR, vol.185, Injection
Laser in Opt.Commun. and Inform. Processing Systems. Nova
Sc.Publishers,N.Y., 1989
- Сандитов Д.С.,Бартенев
Г.М. Физические свойства неупорядоченных структур (Молекулярно-кинетические
и термодинамические процессы в неорганических стеклах и
полимерах). – Новосибирск: Наука, 1982. – 256 с.
- Vigovsky Y.N.,
Malov A.N., Malov S.N.Fetschenko V.S., Konop S.P. //Proc.
SPIE(OIST-97), v.3347(1997) p. 314-324
- Vigovsky Yu.N,
Konop S.P.,.Malov A.N, .Malov S.N. Photoinduced phase transitions
in hologram recording in layers of dichromated gelatin/
Laser Physics, (1998), vol.8, N 4, pp. 901 – 915.
- Выговский Ю.Н.,
Дработурин П.А., Коноп А.Г., Коноп С.П., Малов А.Н. Желатин-глицериновые
“красные” регистрирующие системы с метиленовым голубым.
\\ Компьютерная оптика, (1999), вып. 18, с. 133 – 138.
- Выговский Ю.Н.,
Кручинин Л.Е., Малов А.Н., Малов С.Н., Петров А.А. Лазерный
отжиг коллоидных голографических регистрирующих сред. \\
Компьютерная оптика, (1999), вып. 19, с. 125 – 128.
- Крюков А.И.,
Шерстюк В.П., Дилунг И.И. Фотоперенос электрона и его прикладные
аспекты.–Киев: Наук. Думка, 1982.–240с.
- Гросберг А.Ю.,
Хохлов А.Р. Статистическая физика макромолекул.–М.: Наука,
1989.-344с.
- Габуда С.П.
Связанная вода.–Новосибирск: Наука, 1982,-160с.
- Малов А.Н.,
Малов С.Н., Черный В.В. Физические основы лазерной терапии.
\ Иркутск: ИФ ИЛФ СО РАН, 1997. – препринт № 2. –46 с.
- Проблема белка.
Том 3: Структурная организация белка / Е.М.Попов. – М.:
Наука, 1997. – 604 с
- Волькенштейн
М.В. Общая биофизика. – М.: Наука, 1978. – 592 с.
- Рубин А.Б. .Биофизика.
– М.: Высшая школа, 1987. – 319 + 305 с.
- Романовский
Ю.М., Степанова Н.В., Чернавский Д.С. Математическая биофизика.
– М.: Наука, 1984. – 304 с.
- Малов А.Н.,Малов
С.Н., Черный В.В. Лазерная биостимуляция как самоорганизующийся
неравновесный процесс / Тезисы IV Межд. Конгресса “Проблемы
лазерной медицины” - Москва-Видное, 1997, с.278-279.
- Федер Е. Фракталы.
М., Мир, 1991, 254 стр.
- Малов
А.Н., Костюк М.Г. Модельный анализ основных биологических
процессов в низкоинтенсивной лазерной терапии. \\ Laser
Market, 1995, N 1, с. 37 – 39.
- Oulamara A.,
Tribillon G., Duvernoy J. Biological activity measurement
on botanical speciemen surfaces using a temporal decorrelation
effect of laser speckle. // J. Mod. Opt. – 1989. –36,
N 2. – pp. 165 – 179
- Malov A.N.,
Malov S.N., Feshchenko V.S. Resonance nature of laser biostimulation
from the point of view of quasi-optics.// Laser Physics,
1996, 6, N 5, pp. 979 – 982.
- Эмиссия признака
соматический эмбриодогенез у баклажана. О.О.Тимина, А.Н.Малов,
В.С.Фещенко. \\ “Международный симпозиум по селекции и семеноводству
овощных культур”, РАСХН – М., 1999. С. 354- 359.
- Твердислов В.А.,
Тихонов А.Н., Яковенко Л.В. Физические механизмы функционирования
биологических мембран. / М : МГУ, 1987.
- Аграфонов
Ю.В., Балахчи А.Г., Дорогобид Я.С., Малов А.Н. Влияние структуры
примембранной воды на эффект лазерной биостимуляции. / В
кн.: “Люминесценция и сопутствующие явления”. – Иркутск:
ИГУ, 1999. – с. 65 – 70.
- Gu Qiao. Analogy
between life phenomenon and laser. // Chin. J. Infrared.
Res. A. – 1989.- 8, N 1. – pp. 69 – 74
|
|
|
|
 |
 |
 |
 |
 |
|
Copyright
© 1999-2013 webmaster@media-security.ru
|
|
|


